 English
English









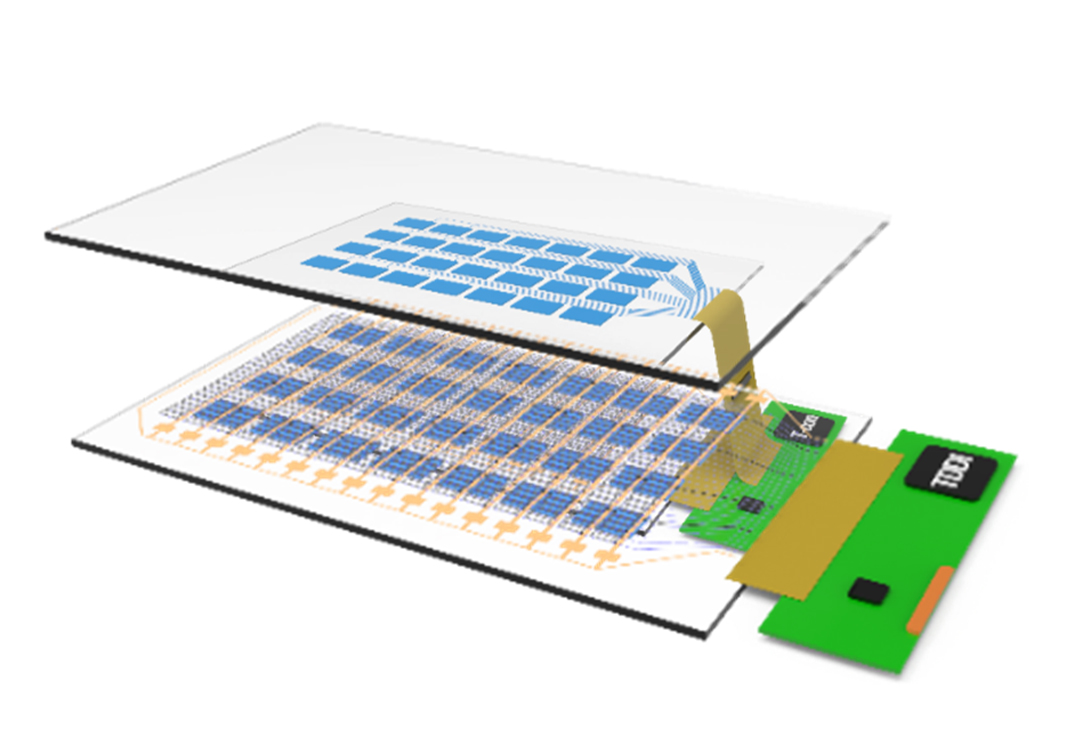

The change of mobility behaviour of users will change and reshape the automotive and industrial industry. The mobility of the future will be much easier, more flexible and more individual for users. BOE Varitronix will continuous
to consolidate our strength, improve our supply stability, enhance our production and technological support which enable the company to have a better competitive advantage to develop our business.